import astropy.units as u
import astropy.constants as const
import matplotlib.pyplot as plt
import numpy as np
def c(rho1, rho2, r1, r2):
return (rho2 * r2) / (rho1 * r1)
def a(r1, r2, c):
return (r1 - r2 * c ** 0.5) / (c ** 0.5 - 1)
def rho0(rho, r1, a):
return rho * (r1 / a) * (1 + r1 / a) ** 2
def rhoNSF(rho0, r, a):
return rho0 / ((r / a) * (1 + r / a) ** 2)
r_h1 = 8.04 * u.kpc
v_h1 = 243.23 * u.km / u.s
r_prcg = 14.95 * u.kpc
v_prcg = 259.26 * u.km / u.s
r_hkg = 16.55 * u.kpc
v_hkg = 261.17 * u.km / u.s
# a) calculate virial mass
m_h1 = r_h1 * v_h1 ** 2 / (2 * const.G)
m_prcg = r_prcg * v_prcg ** 2 / (2 * const.G)
m_hkg = r_hkg * v_hkg ** 2 / (2 * const.G)
print(f"{m_h1.to(u.M_sun):.2e}")
print(f"{m_prcg.to(u.M_sun):.2e}")
print(f"{m_hkg.to(u.M_sun):.2e}")
# b)
rho_h1 = m_h1 / (4 * np.pi * r_h1 ** 3 / 3)
rho_prcg = m_prcg / (4 * np.pi * r_prcg ** 3 / 3)
rho_hkg = m_hkg / (4 * np.pi * r_hkg ** 3 / 3)
d = np.linspace(0, 100, 101) * u.kpc
c_1 = c(rho_h1, rho_prcg, r_h1, r_prcg) # h1 to PRCG
c_2 = c(rho_h1, rho_hkg, r_h1, r_hkg) # h1 to HKG
c_3 = c(rho_hkg, rho_prcg, r_hkg, r_prcg) # HKG to PRCG
a_1 = a(r_h1, r_hkg, c_1)
a_2 = a(r_h1, r_prcg, c_2)
a_3 = a(r_hkg, r_prcg, c_3)
rho0_1 = rho0(rho_h1, r_h1, a_1)
rho0_2 = rho0(rho_h1, r_h1, a_2)
rho0_3 = rho0(rho_hkg, r_hkg, a_3)
rhoNSF_1 = rhoNSF(rho0_1, d, a_1)
rhoNSF_2 = rhoNSF(rho0_2, d, a_2)
rhoNSF_3 = rhoNSF(rho0_3, d, a_3)
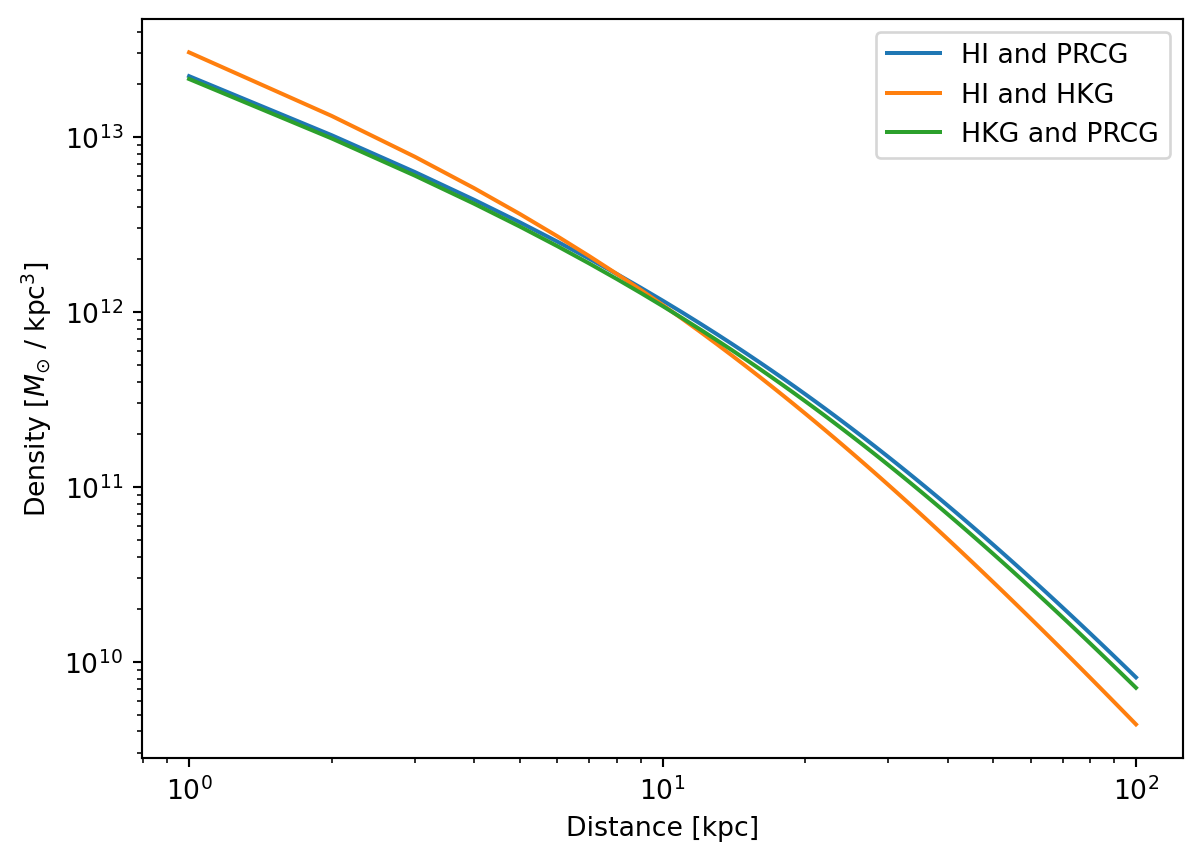
plt.plot(d, rhoNSF_1, label="HI and PRCG")
plt.plot(d, rhoNSF_2, label="HI and HKG")
plt.plot(d, rhoNSF_3, label="HKG and PRCG")
plt.xscale('log')
plt.yscale('log')
plt.legend()
plt.xlabel("Distance [kpc]")
plt.ylabel("Density [$M_{\\odot}$ / kpc$^3$]")
plt.show()